Tema 1(1º). Actividades del tema

https://drive.google.com/open?id=0B4QyheCmYqPHMnFvUWtpWmg0TU0

Temas 1, 2, 3, 4, 5, 6 y 8(1º) Textos que pueden caer para examen (geografía)

https://drive.google.com/file/d/0B4QyheCmYqPHTU9fbTJLV0c2U2s/view?usp=sharing

Tema 1(1º). Movimiento de rotación: datos y actividades de la salida y puesta del sol

Analiza los cuadros de datos que aparecen en esta entrada y responde a las siguientes preguntas:

1. Define los conceptos de orto y ocaso.
2. Indica cuáles de las cuatro fechas señaladas corresponde o se acerca más al solsticio de invierno y justifícalo. Para ello ten en cuenta la duración de las horas de luz y la altura del sol en el cielo.
3. Indica cuáles de las cuatro fechas señaladas corresponde o se acerca más al solsticio de verano y justifícalo. Para ello ten en cuenta la duración de las horas de luz y la altura del sol en el cielo.
4. Indica cuáles de las cuatro fechas señaladas corresponde o se acerca más al equinoccio de primavera y justifícalo. Para ello ten en cuenta la duración de las horas de luz y la altura del sol en el cielo.
5. Indica cuáles de las cuatro fechas señaladas corresponde o se acerca más al equinoccio de otoño y justifícalo. Para ello ten en cuenta la duración de las horas de luz y la altura del sol en el cielo.
6. Teniendo en cuenta el sentido del movimiento de rotación de la Tierra ordena las ciudades señaladas de Este a Oeste. Justifícalo partiendo de las coordenadas de longitud de cada una pero también por las horas de orto y ocaso.

La Coruña (43º 22' 17"N 8º 23' 23"O) AÑO 2013: orto y ocaso (fuente: www.fomento.gob.es/salidapuestasol/2013/Coruna-2013.txt)
	21 de marzo	21 de junio	21 de septiembre	21 de diciembre
ORTO	07:35	06:53	08:20	09:03
OCASO	19:47	22:18	20:33	18:01

Se ha considerado la hora adelantada desde el último domingo de marzo y la hora atrasada

desde el último domingo de octubre.

Córdoba (37º 52' 51"N 4º 46' 44"O) AÑO 2013: orto y ocaso (fuente: www.fomento.gob.es/salidapuestasol/2013/Cordoba-2013.txt)
	21 de marzo	21 de junio	21 de septiembre	21 de diciembre
ORTO	07:21	06:57	08:06	08:31
OCASO	19:32	21:45	20:18	18:03

Se ha considerado la hora adelantada desde el último domingo de marzo y la hora atrasada

desde el último domingo de octubre.

Madrid (40º 24' 35"N 3º 41' 11"O) AÑO2013: orto y ocaso (fuente: www.fomento.gob.es/salidapuestasol/2013/Madrid-2013.txt)
	21 de marzo	21 de junio	21 de septiembre	21 de diciembre
ORTO	07:16	06:45	08:01	08:34
OCASO	19:28	21:48	20:13	17:51

Se ha considerado la hora adelantada desde el último domingo de marzo y la hora atrasada

desde el último domingo de octubre.

Barcelona (41º 23' 7"N 2º 10' 39"E) AÑO 2013: orto y ocaso (fuente: www.fomento.gob.es/salidapuestasol/2013/Barcelona-2013.txt)
	21 de marzo	21 de junio	21 de septiembre	21 de diciembre
ORTO	06:53	06:18	07:38	08:14
OCASO	19:05	21:28	19:50	17:25

Se ha considerado la hora adelantada desde el último domingo de marzo y la hora atrasada

desde el último domingo de octubre.

Palma de Mallorca (39º 34' 20"N 2º 39' 11"E) AÑO 2013: orto y ocaso (fuente: www.fomento.gob.es/salidapuestasol/2013/Palma-2013.txt)
	21 de marzo	21 de junio	21 de septiembre	21 de diciembre
ORTO	06:51	06:22	07:36	08:06
OCASO	19:02	21:20	19:48	17:29

Se ha considerado la hora adelantada desde el último domingo de marzo y la hora atrasada

desde el último domingo de octubre.

Tema 1(1º). Texto sobre los calendarios juliano y gregoriano: años bisiestos

Para que las cosas funcionen bien tenemos que encajar el calendario astronómico -el que marca la posición de equinoccios y solsticios- con el calendario civil y religioso, basado en días completos. Y es que el tiempo que tarda la Tierra en dar una vuelta alrededor del Sol -un año- no es un múltiplo exacto de rotaciones sobre sí misma -un día-. En concreto, un año astronómico (año ‘trópico’) dura 365 días, 5 horas y casi 49 minutos. El problema de relacionar años con días completos fue bastante bien resuelto por el romano Julio César y sus sabios egipcios allá por el año 50 antes del propio Cristo. Como en números redondos un año son 365 días y un cuarto, cada cuatro años de 365 días habría de añadirse un día adicional (el famoso bisiesto, como es este de 2016). Y así hemos funcionado bastante bien durante muchos siglos, con el propiamente llamado calendario ‘juliano’, hasta que los hechos toparon con la realidad.

La corrección romana contenía un pequeño error intrínseco, puesto que redondeaban las 5 horas y 49 minutos a las 6 horas. Esto significaba que cada año se introducían en el calendario unos 11 minutos de más, por lo que poco a poco se iba alejando del astronómico. En el siglo XVI, el error acumulado era tal que el equinoccio primaveral -supuestamente, el 21 de marzo- había ocurrido el 11 de marzo, diez días antes. Y continuaba subiendo. Para resolver este desaguisado, el papa de turno, Gregorio XIII, recurrió de forma conjunta a Dios y a las matemáticas, confluyendo por fortuna estos factores en el enorme astrónomo -tanto por su tamaño físico como por su sabiduría-, Christopher Clavius. Clavius, alemán y jesuita, fue coetáneo y amigo de Galileo, con quien tuvo sus más y sus menos al respecto de sus muy distintas concepciones del Universo, puesto que se mantuvo siempre fiel al geocentrismo.

Corrigió de forma ingeniosa el calendario juliano, y lo hizo añadiendo una cláusula adicional: “Un año será bisiesto si es divisible por 4, pero no lo será si además es divisible por 100. Con la excepción de los divisibles por 100 y 400 a la vez, que sí lo serán”. Pongamos un ejemplo sencillo: el año 1900 no fue bisiesto, como no lo será el 2100, pero sí lo fue el más reciente año 2000. Para rematar su trabajo, el papa Gregorio -por indicación del gran Clavius- tuvo que resetear el calendario mediante la pertinente bula, eliminando de golpe los diez días de más acumulados hasta esa fecha, y así al jueves 4 de octubre de 1582 (del calendario juliano) le siguió el viernes 15 de octubre de 1582 (del calendario ya conocido como ‘gregoriano’). El trabajo de Clavius fue tan bueno que perdura hoy en día y solo tiene un error estimado de un día cada 3.300 años.
http://elpais.com/elpais/2016/01/25/ciencia/1453735339_015453.html

«Christopher Clavius» por Francesco Villamena - Immediate source: http://www.sil.si.edu/digitalcollections/hst/scientific-identity/fullsize/SIL14-C4-02a.jpg (note engraving has "CHRISTOPHORVS CLAVIVS BAMBERGENSIS" and "Franciscus Villamoena Fe. Rome Anno 1606")
Ultimate source: A 16th century engraving after a painting by Francisco Villamena. (source for artist: [1]). Disponible bajo la licencia Dominio público vía Wikimedia Commons.

Tema 1(1º). Texto sobre las proyecciones cartográficas

Mercator y el mapa que ‘cuadró el círculo’

Con tecnología de hoy en día, capaz de digitalizar casi cualquier cosa, representar el mundo en mapa plano y que este sea fiel al cien por cien sigue siendo un reto pendiente. Este problema matemático tiene muchos siglos de antigüedad. Sin embargo, no fue hasta mediados del siglo XVI cuando Gerardus Mercator (1512-1594) puso la primera piedra para mejorar la representación gráfica del planeta Tierra en una superficie de dos dimensiones.

A su solución, que él aplicó por primera vez en 1569, se la conoce como Proyección de Mercator (proyección cilíndrica). Aunque actualmente se critica como símbolo de las desigualdades geográficas y de la arrogancia del primer mundo (África y Sudamérica se ven mucho más pequeñas de lo que son) la intención de Mercator era muy distinta. En realidad, lo que pretendía era facilitar la navegación de los marineros de la época, al diseñar un sistema en el que las trayectorias de los barcos pudieran trazarse en línea recta con las brújulas.

Las proyecciones de tipo cilíndrico, como la de Mercator basan su representación en colocar un cilindro tangente a la esfera terrestre. El resultado muestra todo el globo en dos dimensiones, pero también presenta grandes distorsiones en las zonas de latitud elevada, cosa que impide apreciar en sus verdaderas proporciones a las regiones polares. Así, en los mapas basados en el sistema de Mercator, Groenlandia aparece casi tan grande como África, que en realidad es unas 14 veces mayor; o Alaska aparece similar en tamaño a Brasil, cuya área es casi 5 veces la de Alaska.

"Mercator projection SW" by Strebe - Own work. Licensed under CC BY-SA 3.0 via Commons.

La proyección de Peters es otra famosa representación cilíndrica, que muestra de manera más equilibrada la proporción de tamaño de los continentes pero que tiene otro fallo: las superficies y distancias están deformadas. Otros sistemas resuelven el problema de la proporción, pero nos dan una imagen “limitada” del globo: las proyecciones cónicas representan de manera fiel aquellos países que se encuentran en las regiones de latitudes medias pero que no muestran el total del globo en un mismo papel.

«Gall–Peters projection SW» por Strebe - Trabajo propio. Disponible bajo la licencia CC BY-SA 3.0 vía Wikimedia Commons.

En la actualidad la mayoría de los mapas se basan en proyecciones modificadas o en una combinación de las anteriores, para corregir en lo posible las distorsiones. Entre las más usuales figuran la proyección policónica de Lambert, utilizada para fines educativos, o la de Winkel-Tripel, adoptada por la National Geographic Society en 1998 y cada vez más utilizada en atlas y libros de texto. Sin embargo, los mapas más utilizados hoy en día siguen fieles a Gerardus Mercator: los servicios online como Bing Maps, OpenStreetMap, Google Maps o MapQuest usan una variante de la proyección de Mercator. Y también los mapas rectangulares que se hacen hoy en día de otros mundos (Venus, Marte, o Mercurio por ejemplo) usan el sistema de Gerardus Mercator.

«Winkel-tripel-projection» por NASA - NASA. Disponible bajo la licencia Dominio público vía Wikimedia Commons.

Este astrónomo, geógrafo y matemático flamenco dedicó toda su vida a los mapas. Combinando sus diferentes especialidades, realizó aportaciones muy diversas a la cartografía. La más importante de ellas, su solución al problema de llevar a un plano el globo terráqueo, pese a ser una solución imperfecta sigue siendo muy útil y práctica. Por eso la tan denostada proyección de Mercator sigue plenamente vigente.

Ventana al Conocimiento

www.bbvaopenmind.com/mercator-y-el-mapa-que-cuadro-el-circulo/

Tema 1(1º). Texto sobre las reproducciones a escala de la Tierra

Cuestiones sobre el texto:

1. ¿Cómo representan los globos y los mapas la Tierra?
2. ¿Cuál es la definición de escala que nos da el texto?
3. ¿Cuál es la ventaja de representar la escala mediante una fracción?
4. ¿Cuál es la escala que se utiliza más comúnmente?
5. Si la escala 1 cm: 650 km no se puede representar en forma de fracción al ser medidas distintas. ¿Con qué otro tipo de escala se puede representar?

Todos los globos y mapas representan las características de la tierra a un tamaño mucho menor que el que poseen en realidad. Los globos están pensados en principio para ser modelos perfectos de la tierra, diferenciándose de ella únicamente en tamaño, pero manteniéndose las formas. la escala de un globo será, por tanto, la relación entre el tamaño del globo y el tamaño de la tierra, tamaño que debe ser expresado en alguna medida de longitud o distancia (pero no de área o volumen). Tomemos, por ejemplo, un globo de 20 cm de diámetro que represente la tierra. cuyo diámetro real se acerca a los 13.000 km. La escala del globo será la relación entre 20 cm y 13.000 km. Di dividimos 13.000 entre 20, podremos expresar la escala de la siguiente forma: 1 cm sobre el globo representa 650 km en la realidad. Esta afirmación es válida para determinar la distancia entre dos puntos cualquiera del globo.

La escala se utiliza más comúnmente como una fracción simple que se obtiene expresando las distancias del globo y de la tierra en la misma unidad de medida, en este caso en centímetros:

1 cm en el globo : 650 km en la tierra = 1 cm : 650x100.000 = 1 : 65.000.000

La ventaja de este sistema de representar la escala a través de una fracción, es que es totalmente independiente de las unidades de medida, siendo válida para pies, millas, metros, kilómetros o cualquier otra unidad. Sea cual sea su nacionalidad, cualquier persona puede comprender esa fracción, independientemente de su idioma o de las unidades de medida que utilice.

STRAHLER, Arthur N. y STRAHLER, Alan H., Geografía Física, Barcelona, Ediciones Omega, 1989, p. 9

«Behaim Globus» per Pirkheimer - Treball propi. Disponible sota la llicència CC BY-SA 3.0 via Wikimedia Commons.

Temas 1(1º). Texto sobre la esfericidad de la Tierra (Texto adaptado)

"The Earth seen from Apollo 17" door NASA/Apollo 17 crew; taken by either Harrison Schmitt or Ron Evans - http://www.nasa.gov/images/content/115334main_image_feature_329_ys_full.jpg
Alt: http://grin.hq.nasa.gov/ABSTRACTS/GPN-2000-001138.html (direct link). Licentie Public domain via Wikimedia Commons.

En la época de los satélites artificiales, la forma esférica de la tierra es un hecho evidente que tendríamos dificultades en imaginarnos a nosotros mismos viviendo en los tiempos en que la extensión y configuración de la tierra eran completamente desconocidas. En aquellos tiempos, los navegantes que atravesaban el Mediterráneo veían la superficie del mar perfectamente lisa, acabándose en un horizonte circular. Basándose en esta percepción habían deducido que la tierra tenía forma de un disco plano y, por ello, si navegaban en dirección a sus bordes, los barcos acabarían por caer en algo desconocido. Sin embargo, esos mismos navegantes esos mismos navegantes podrían haber percibido que la superficie de la tierra no es plana sino curvada, como una pequeña parte de una esfera, a través de la observación de que el sol ilumina las cimas de las nubes y de las montañas altas antes de la salida del sol y después de su puesta.

Una prueba de la esfericidad de la tierra puede hallarse a partir de las observaciones en el mar. Cuando un barco se aleja más y más en la costa, parece que se hunde lentamente por debajo del nivel del mar. Visto a través de los prismáticos o de un telescopio, la superficie del mar parecerá ascender hasta que las cubiertas estén inundadas, y, entonces, gradualmente se sumergirán la chimenea y los mástiles hasta que al final sólo el humo sea visible sobre el horizonte.

STRAHLER, Arthur N. y STRAHLER, Alan H., Geografía Física, Barcelona, Ediciones Omega, 1989, pp. 3 y 4.

"Shiphorp" by Anton - Own work. Licensed under CC BY-SA 2.5 via Wikimedia Commons.

Tema 1(1º). Texto adaptado sobre los mapas y su representación

Se entiende inicialmente que un mapa representa en un espacio reducido información espacial a escala. Se espera que un mapa ponga al alcance de nuestra mirada información y aspectos de un territorio que no conoceríamos si no lo recorriéramos o exploráramos.

Los mapas ayudan a recorrer territorios (un mapa me ayuda a ir de un punto de la ciudad al otro), tanto como a evitar el tener que recorrerlos (no tengo que ir a explorar la Selva Amazónica y los Andes para saber en qué país nace el río Amazonas). Para recorrer un territorio necesitamos un mapa y para hacer un mapa necesitamos recorrer el territorio.

Los mapas ayudan en el dominio y control del territorio (militarmente, infraestructuras, turísticamente...) proporcionando los mecanismos de hacerlo, llegando incluso a simbolizar el hecho mismo de que es territorio ha sido dominado y explorado (puesto que para trazar un mapa hay que haberlo recorrido).

Al ver un mapa de un territorio no se puede experimentar la dimensión del mismo, qué tan grande o pequeño es, pero sí conocer la disposición de los elementos que hay en ese territorio.

Los mapas tienen muchas funciones, la representación del territorio es sólo una de las opciones. Los mapas también representan distintos tipos de datos: políticos, físicos, económicos...

En la historia de la elaboración y creación de mapas del globo terráqueo se pueden reconocer algunas fases:

• Fase 1. La imaginación es la protagonista en los mapas. No son utilizados para recorrer el mundo sino para explicarlo, para narrarlo, para mostrar la visión religiosa o política que tiene el autor de él.
• Fase 2. En esta fase ya el mapa es imprescindible para explorar, recorrer (principalmente por mar) y dominar las distintas zonas del mundo. Debido a dificultades técnicas y existencia de regiones inexploradas los mapas de los territorios de mayor escala tienen abundantes inexactitudes y distorsiones de ángulos y escalas.
• Fase 3. Por fin se ha alcanzado un alto nivel técnico y teórico en su elaboración. Sin embargo al intentar ubicar de forma exacta la información distribuida sobre el geoide, el mapa plano siempre muestra distorsión con respecto a la realidad (los ángulos cambian, las paralelas dejan de serlo, las distancias se modifican…). Es por ello que se hace preciso elegir una proyección particular, con su sistema matemático, según las necesidades. Como cada proyección representa mejor unas zonas del globo que otras se elegirá en función del territorio que se quiere representar y de los datos que se quieren mostrar.

Los mapas ya no son lo que eran. Ahora todo es "mapeable", ya que ahora todo es "datable" y, en el mismo orden de ideas, tratable estadística y científicamente. La rápida divulgación de las imágenes gracias a internet y otros factores más técnicos exigen cada vez mayor sofisticación. También las nuevas formas científicas y cierta cultura científica divulgativa han dado lugar una especie de arte o interés artístico de la representación científica. El mapa ya no sólo es usado sino también admirado.

moebio.com/santiago/textos/transtextos/mapas.html

Ejemplo de fase 1. «Anaximander world map-es» por User:Bibi Saint-Pol - Own work (original PNG version by User:Gwwfps is/was : en:Image:Anaximandermap.png, based on an image found in An Introduction to Early Greek Philosophy by John Mansley Robinson, Houghton and Mifflin, 1968, ISBN 0395053161).. Disponible bajo la licencia Public domain vía Wikimedia Commons.

Ejemplo de fase 2. «Delisle - Mappe-Monde» por Guillermo Delisle - Este archivo no tiene información sobre su origen.
Por favor edita su descripción e añade una fuente.. Disponible bajo la licencia Public domain vía Wikimedia Commons.

Ejemplo de fase 3. «Robinson projection SW» por Strebe - Trabajo propio. Disponible bajo la licencia CC BY-SA 3.0 vía Wikimedia Commons.

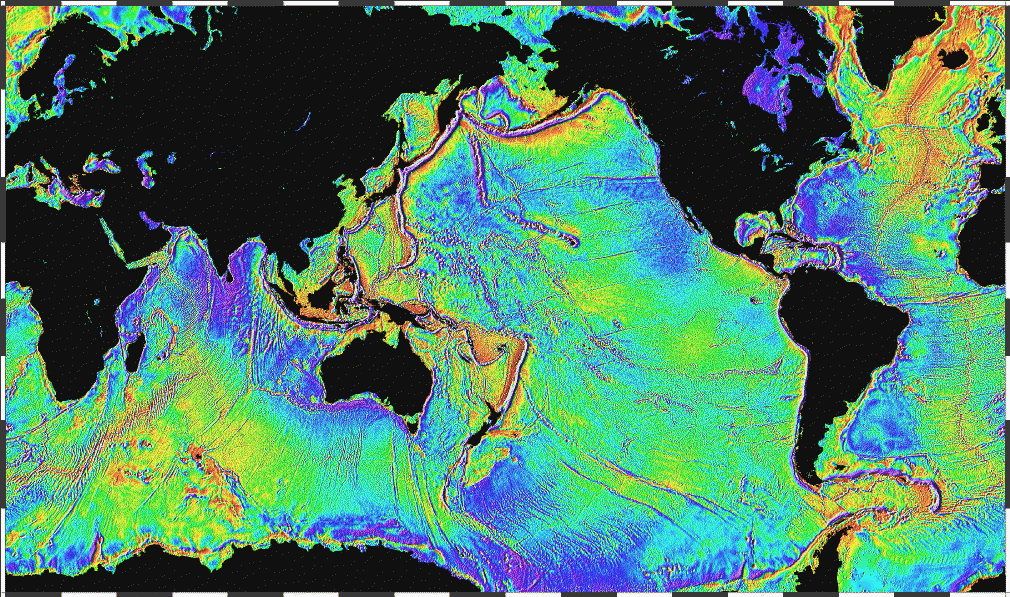Mapa divulgativo actual "Ocean gravity map" by NOAA - http://www.ngdc.noaa.gov/mgg/bathymetry/predicted/explore.HTML. Licensed under Public domain via Wikimedia Commons.

Mapa divulgativo actual. blog.berde-berdea.net/es/baliabideak-recursos/kutsadura-contaminacion/argi-kutsaduraren-munduko-mapa/

Tema 1(1º). La posición del Sol en el Horizonte

Debido a la inclinación del eje terrestre el Sol aparece inclinado en el horizonte. Dicha inclinación es mayor durante la estación invernal y menor durante los meses estivales. Igualmente cuanto mayor es la latitud mayor es la inclinación del Sol en el horizonte. Si te encuentras en el Hemisferio Norte la inclinación del Sol en el horizonte será hacia el Sur. Si por el contrario te encuentras en el Hemisferio Sur la inclinación del mismo será hacia el Norte.

Os presento una imagen que lo muestra claramente. Igualmente os incluyo un texto en el que se puede constatar la reacción los antiguos griegos y fenicios ante las diferencias en el Hemisferio Norte y Sur anteriormente señaladas.

Posición del sol, sombra y horas del amanecer y atardecer, según el sosticio o el equinoccio. Fuente: «Solstice and Equinox» por Slancestoene.png: Златко Кръстев/Zlatko Krastev
derivative work: Mjchael (talk) - Slancestoene.png. Disponible bajo la licencia GPL vía Wikimedia Commons.

Cuestiones sobre el texto:

1. ¿Quién era Herodoto? ¿Por qué no se cree que los fenicios han circunvalado África?
2. ¿En qué hemisferio vivía Herodoto, los griegos y los fenicios? ¿Dónde está el sol de mediodía en ese hemisferio?
3. ¿Por qué creemos como posible que los fenicios hubiesen rodeado la costa africana? Razona tu respuesta.
4. ¿Qué es el mediodía? ¿Dónde se encuentra el sol del mediodía en el Hemisferio Sur?
5. Indica los adjetivos de los puntos cardinales que aparecen en el texto.

<<En dirección al Sur, los navegantes fenicios hicieron viajes aún más notables. Pagados por un rey egipcio, exploraron las costas africanas e hicieron la circunnavegación completa de este gigantesco continente. La única noticia que tenemos de esto se halla en las obras del historiador griego Heródoto, obras escritas dos siglos después.>>

>>Heródoto no creía el relato de los fenicios porque éstos afirmaban que en el extremo meridional de África el sol de mediodía aparecía en la región septentrional del cielo. Puesto que el sol de mediodía siempre estaba hacia el Sur, cuando se lo contemplaba desde Grecia o de cualquier tierra mediterránea, Heródoto pensó que esto era una ley invariable de la naturaleza, que los fenicios mentían y, por tanto, que habían inventado toda la historia.>>

>>El extremo meridional de África está en la Zona Templada del Sur, desde donde el sol de mediodía siempre se ve realmente hacia el Norte. El mero hecho de que los fenicios describiesen este hecho aparentemente imposible nos dice que realmente estuvieron allí y probablemente circunnavegaron África.>>

ASIMOV, Isaac, La tierra de Canaan, Madrid, Alianza Editorial, 1987 p. 138

Tema 1(1º). Mitología y arte: el nacimiento de la Vía Láctea

Para los antiguos las estrellas del cielo estaban relacionadas con sus dioses y diosas. Ese fue, por supuesto, el caso de los antiguos griegos. Para la mitología griega el nacimiento del conjunto de estrellas que conforman nuestra galaxia ocurrió de la siguiente manera.

El dios Zeus, el rey de los dioses, tuvo un hijo con una mortal al que llamaron Herakles (Hércules para los romanos). Buscando que su hijo semidios recién nacido fuese también inmortal Zeus intentó que fuera amamantado por su divina esposa Hera mientras esta dormía. Sin embargo el niño tenía tal fuerza que la diosa al despertarse apartó al niño y la leche salió desparramada por el espacio dando lugar a esa sucesión de estrellas llamada la Vía Láctea (camino de leche).

Ahora nuestra galaxia, de la cual forma parte nuestro Sistema Solar, recibe el nombre de Vía Láctea.

La temática sobre el nacimiento de la Vía Láctea fue recogido por el pintor barroco flamenco Pedro Pablo Rubens en un cuadro de 1636 que se encuentra en el Museo del Prado de Madrid.

Peter Paul Rubens, El nacimiento de la Vía Láctea, 1636. Fuente: «Rubens Vía Láctea» por Peter Paul Rubens - https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhxw2b30THI4A0QjCGH1VY-D1ytqSkwRo9b_vniU9K-e1yAuDgFK5wNVlcs75gS0feyx6lLSZxxxobEmsHTNmbc2H60p7L6v4y71hTGLWSDFdDETeGUt8qUu7NWavhca2u_8_mV169MIQ/s1600/ruben_vialactea.jpg, 2012-01-17. Disponible bajo la licencia Public domain vía Wikimedia Commons.

Tema 1(1º). Proyecciones cartográficas

Proyección Cilíndrica o Mercator. Para ver su distorsión con respecto a la realidad fijaros en los paralelos y en los meridianos en la cercanía de los polos.

Proyección Cónica. Para ver su distorsión con respecto a la realidad fijaros en los paralelos y en los meridianos en la cercanía del Ecuador.

Enlace con original: commons.wikimedia.org/wiki/File:Projection_conique.jpg

Proyección Cenital.

Enlace con el original: commons.wikimedia.org/wiki/File:Projection_azimutale_gnomonique.jpg

Tema 1(1º). Coordenadas geográficas (modelo y ejercicio)

Para situar un punto en un mapa necesitamos las coordenadas geográficas.

• Recuerda que tenemos que poner la numeración de un paralelo en grados (LATITUD) y la numeración de un meridiano en grados (LONGITUD).
• Recuerda también que los paralelos que se encuentran al Norte del Ecuador (paralelo 0º) son latitud grados Norte (ºN) y los paralelos al Sur del Ecuador (paralelo 0º) son latitud grados Sur (ºS).
• Igualmente los meridianos que se encuentran al Este del Meridiano de Greenwich (meridiano 0º) son longitud grados Este (ºE) y los meridianos que se encuentran al Oeste del Meridiano de Greenwich (meridiano 0º) son longitud grados Oeste (ºO).
• Finalmente no te olvides que en las coordenadas va primero la latitud y luego la longitud. Ejemplo 30ºN 20ºE.

AVERIGUA LAS COORDENADAS DE LOS PUNTO A, B, C, D, E y F. (enlace documento PDF)

Tema 1(1º). Solsticios, equinoccios y estaciones

Solsticios, equinoccios y estaciones is licensed under a Creative Commons Reconocimiento 4.0 Internacional License.

Temas 1(1º). Texto sobre el Sistema Solar: su reproducción a escala

Antes de empezar a leer este texto a lo mejor deberías saber lo que es la "escala": es la reproducción (dibujo, maqueta...) de algo real de forma proporcional (aunque es más pequeño la reproducción en la realidad todo tiene que ser igual de pequeño con respecto a ella). Ejemplo, un coche de juguete es una reproducción en pequeño de la realidad; todo está al mismo tamaño de reducción (rueda, puertas, volante...). Para cualquier ampliación en este blog hay una entrada sobre esa cuestión: socialesmoriles.blogspot.com.es/2011/09/tema-2-escalas-de-mapas.html

<<[...] Te darás cuenta también enseguida de que ninguno de los mapas que hayas podido ver del sistema solar estaba dibujado ni siquiera remotamente (lejanamente) a escala. La mayoría de los mapas que se ven en las clases muestran los planetas uno detrás de otro a intervalos (distancias) de buena vecindad (relativamente cercanos unos de otros) -los gigantes exteriores (Júpiter, Saturno, Urano y Neptuno) llegan incluso a proyectar sombras unos sobre otros en algunas ilustraciones-, pero se trata de un engaño necesario para poder incluirlos todos en la misma hoja. En verdad, Neptuno no está un poquito más lejos que Júpiter. Está mucho más allá de Júpiter, cinco veces más que la distancia que separa a Júpiter de la Tierra, tan lejos que recibe solo un 3% (por cada 100 que recibe Júpiter, Neptuno solo recibe 3) de la luz que recibe Júpiter. Las distancias son tales, en realidad, que nos es prácticamente imposible dibujar a escala el sistema solar. Aunque añadieses montones de páginas plegadas a los libros de texto o utilizases una cartulina realmente grande no podrías aproximarte siquiera. En un dibujo a escala del sistema solar, con la Tierra reducida al tamaño de un guisante, Júpiter estaría a trescientos metros de distancia (aproximadamente trescientos pasos) y, Plutón, a 2,5 kilómetros (aproximadamente a 2.500 pasos) [...].>>

BRYSON, Bill, Una breve historia de casi todo, Barcelona, RBA Libros, 2005.

Tema 1(1º). Curvas de nivel

Os incluyo un enlace sobre curvas de nivel. Visitadlo tiene majores gráficos que los que yo os pongo aquí.

También os incluyo una breve explicación sacada de la ENCICLOPEDIA DEL ESTUDIANTE, "05 Geografía General", 2005, El País, página 273.

<<El método más utilizado actualmente para representar el relieve es el de las curvas de nivel. Es el que se usa en los mapas topográficos, en los que siempre debe plasmarse el relieve de alguna forma.

Una curva de nivel es una línea imaginaria dibujada en los mapas para señalar los lugares terrestres que están a la misma altitud. La altitud es la altura sobre el nivel del mar. Si se pudiera caminar sobre una curva de nivel se estaría andando a una altitud constante, sin subir ni bajar.

En un mapa, las curvas de nivel:

• Indican la forma, inclinación y altitud del terreno.
• En general, se dibujan en color marrón en los continentes y de color azul en el mar.
• Siempre se trazan cerradas como el resto de las isolíneas, aunque pueda parecer que no lo están.
• Son equidistantes, es decir, la distancia que separa dos curvas de nivel consecutivas es siempre igual, y, además, representa la diferencia de altitud entre ambas. [...]>>

Enlace con http://recursos.cnice.mec.es/biosfera/alumno/3ESO/energia_externa/contenidos14.htm

Tema 1(1º). Escalas de mapas

Cualquier reducción del tamaño de un objeto o superficie con respecto al original (en tamaño original) se llama "reducción a escala". La reducción del tamaño de la reproducción con respecto al original deberá ser proporcional para que así su parecido con la realidad sea lo más creible posible. Un ejemplo es la fotografía que os incluyo a continuación,  en la que aparece una reproducción de una locomotora de ferrocarril a una escala 1:87. Ello significa que la reproducción es 87 veces más pequeña que el original y que para conocer las medidas del original solo es preciso multiplicar cualquier medida de la reproducción por 87.

 

Esta reproducción de un transatlántico es de una escala 1:100 con respecto al original.

 

El globo terráqueo es una reproducción a escala o proporcional de la Tierra que suele ser de alrededor de 1:40.000.000.

 

En los mapas ocurre lo mismo: un mapa es una reproducción proporcional (más o menos perfecta) de la realidad o del espacio. Ello significa que un mapa 1:50.000 es una reproducción de un territorio en una proporción 50.000 más pequeña que la realidad. Vamos, que es 50.000 veces más pequeño. Para conocer las distancias de la realidad, sólo hay que medir la distancias de la reproducción (el mapa) y multiplicarlo por 50.000. El mismo principio es válido para mapas 1:2.600.000 o cualquier otra escala.

Os incluyo al final un enlace con una página del Ministerio de Educación donde se plantéan unas orientaciones sencillas para calcular la distancia en la realidad partiendo de las distancias en un mapa.

También os incluyo la explicación sacada de la ENCICLOPEDIA DEL ESTUDIANTE, "05 Geografía General", 2005, El País, página 271.

<<La escala es la proporción existente entre la dimensión de un territorio en la realidad y la dimensión que el corresponde en el mapa. La escala indica el número de veces que se ha reducido el tamaño de la superficie real y es un elemento fundamental en los mapas. [...]>>

ENLACE CON http://recursos.cnice.mec.es/biosfera/alumno/3ESO/energia_externa/contenidos13.htm

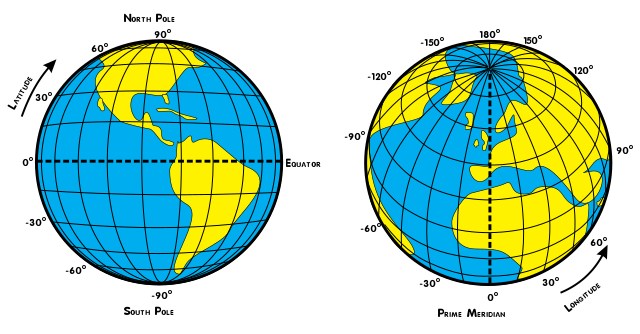
Tema 1(1º). Latitud y longitud: las coordenadas geográficas.

Conceptos:

1. Latitud. Es la distancia desde cualquier punto de la Tierra al Ecuador (paralelo 0º). Como por cada punto de la Tierra pasa un paralelo y estos se enumeran en grados, entonces la latitud se expresa en grados. Pueden ser grados Norte (ºN) si los paralelos se encuentran al Norte del Ecuador o grados Sur (ºS) si los paralelos se encuentran al Sur del Ecuador.
2. Longitud. Es la distancia desde cualquier punto de la Tierra al Meridiano de Greenwich (meridiano 0º). Como por cada punto de la Tierra pasa un meridiano y estos se enumeran en grados, entonces la longitud se expresa en grados. Pueden ser grados Oeste (ºO) si los meridianos se encuentran al Oeste del Meridiano de Greenwich o grados Este (ºE) si los meridianos se encuentran al Este del Meridiano de Greenwich.
3. Coordenadas geográficas. 

• La latitud y la longitud constituyen las coordenadas geográficas 
• Sirven para localizar un punto en la superficie terrestre.
• En realidad los paralelos y meridianos constituyen una malla que se entrecruzan entre sí. Con citar el meridiano y el paralelo que se entrecruzan en un punto tendremos la situación de ese punto. 
• Por ejemplo las coordenadas de Moriles son más o menos  37ºN, 4ºO. Lo que significa que se encuentra en el paralelo (más o menos) 37º al Norte del Ecuador y el meridiano (más o menos) 4º al Oeste del Meridiano de Greenwich.

 Incluyo ahora dos enlaces para prácticar con coordenadas geográficas:

ENLACE CON EDUCAPLUS.ORG: LATITUD Y LONGITUD

ENLACE CON EDUCAPLUS.ORG: COORDENADAS GEOGRÁFICAS

Tema 1(1º). Meridianos

Meridianos:

1. Son líneas imaginarias trazadas de Norte a Sur, de polo a polo. Se puede decir que dividen la Tierra en algo parecido a los gajos de una naranja.
2. El meridiano de referencia o meridiano 0º es el conocido por el nombre de Meridiano de Greenwich. Tiene una longitud exactamente igual al resto de los meridianos.
3. A partir del Meridiano de Greenwich se ordenan los restantes. Los meridianos se empiezan a contar a partir del Meridiano de Greenwich en dos direcciones: hacia el Oeste (ºO) y hacia el Este (ºE).
4. Los meridianos son la referencia de los husos horarios y las zonas horarias de la Tierra.

Tema 1(1º). La Rosa de los Vientos

Es fundamental para nuestro trabajo en geografía que conozcamos la Rosa de los Vientos. Dibujadla en vuestro cuaderno y memorizadla. Hay que saber donde están el Norte, Sur, Este y Oeste. Sobre todo para orientarnos con un mapa.

ENLACE CON EDUCAPLUS.ORG: JUEGO PARA SITUAR LOS PUNTOS CARDINALES DE LA ROSA DE LOS VIENTOS

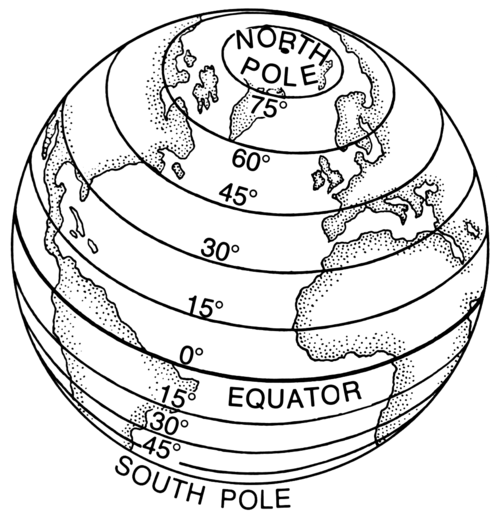
Tema 1(1º). Paralelos

Paralelos

1. Son líneas imaginarias que rodean la Tierra y que son paralelas al Ecuador.
2. El Ecuador es el paralelo 0º, tiene la mayor circunferencia y rodea Tierra en el punto de mayor circunferencia.
3. El Ecuador divide la Tierra en dos Hemisferios (Norte y Sur). Los paralelos se empiezan a contar a partir del Ecuador en dos direcciones: hacia el Norte (ºN) y hacia el Sur (ºS).
4. Los paralelos más importantes son: Trópico de Cancer, Trópico de Capricornio, Círculo Polar Ártico y Círculo Polar Antártico.

ENLACE CON LA PÁGINA EDUCAPLUS.ORG: JUEGO PARA SITUAR LOS PRINCIPALES PARALELOS